This is probably the most efficient structure for implementing a Hilbert transform. Actually, it’s not a Hilbert transform, but two all-pass IIR filters whose phase difference is approximately 90 degrees over a range of frequencies symmetric around Nyquist/2. Laurent de Soras uses these kind of filters in his HIIR resampling library. This note is available in Maple format: hilbert.mws
2003/07
90 degree phase difference IIR allpass pair
> H_sect := (z, a) -> (a^2 – z^(-2)) / (1 – a^2 * z^(-2));
![[Maple Math]](./Hilbert transform_files/hilbert1.gif)
Equation 1. Allpass section taking one multiplication when a^2 is a known coefficient.
We construct two allpass filters from such sections:
![[Maple Math]](./Hilbert transform_files/hilbert2.gif){kind=small}
Equation 2. First allpass filter, delayed by one sample.
![[Maple Math]](./Hilbert transform_files/hilbert3.gif){kind=small}
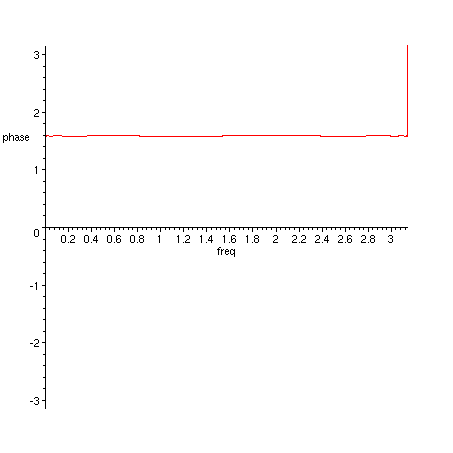
> plot({argument(H_1(exp(I*freq))), argument(H_2(exp(I*freq)))}, freq=0..Pi, phase = -Pi..Pi);
Figure 1. Phases of H_1 (red) and H_2 (green).
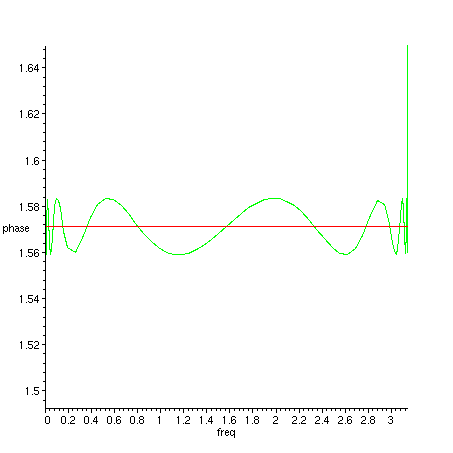
> plot(argument(H_2(exp(I*freq))/H_1(exp(I*freq))), freq=0..Pi, phase = -Pi..Pi);
Figure 2. Phase difference of H_2 and H_1.
Figure 3. Phase difference of H_2 and H_1 (green), detail near 90 degrees (red).
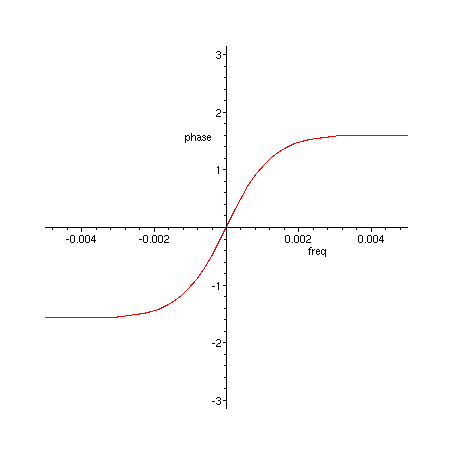
> plot(argument(H_2(exp(I*freq))/H_1(exp(I*freq))), freq=-0.005..0.005, phase = -Pi..Pi);
Figure 4. Phase difference of H_2 and H_1, detail near 0 Hz.
> H := z -> 0.5*(H_2(z)+I*H_1(z));
![[Maple Math]](./Hilbert transform_files/hilbert8.gif){kind=small}
Equation 4. Combined complex filter that will remove negative frequencies.
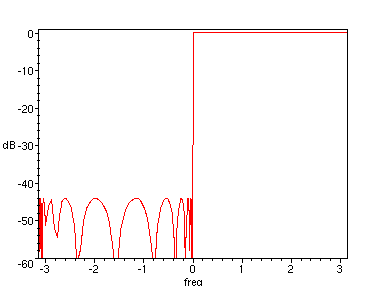
> plot(20*log10(abs(H(exp(I*freq)))), freq=-Pi..Pi, dB=-60..1, axes=boxed);
Figure 5. Frequency response of filter in Equation 4.
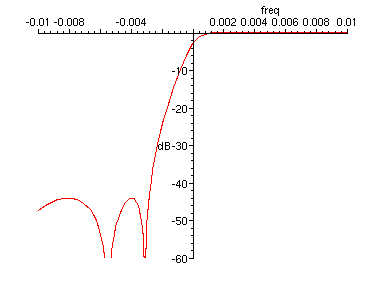
> plot(20*log10(abs(H(exp(I*freq), 0.4))), freq=-0.01..0.01, dB=-60..1);
Figure 6. Frequency response of filter in Equation 4, transition band detail
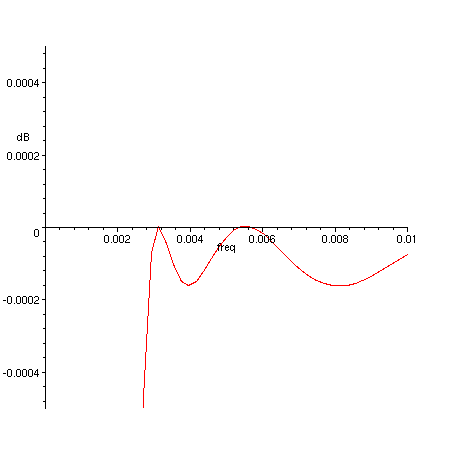
> plot(20*log10(abs(H(exp(I*freq), 0.4))), freq=0..0.01, dB=-0.0005..0.0005);
Figure 7. Frequency response of filter in Equation 4, transition band – passband detail.
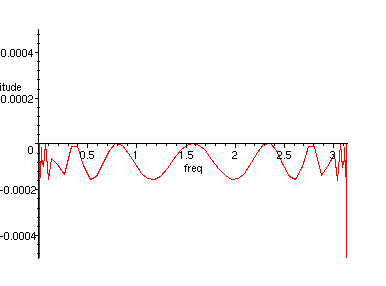
> plot(20*log10(abs(H(exp(I*freq)))), freq=0..Pi, magnitude=-0.0005..0.0005);
Figure 8. Frequency response of filter in Equation 4, passband detail
Plenty cheap for a total of 8 multiplications (plus final scaling by 0.5)!
The coefficients were found using a generic evolutionary algorithm. I believe that it would be possible to design coefficients for this filter structure using the software by Artur Krukowski, which finds coefficients for halfband filters: http://www.cmsa.wmin.ac.uk/~artur/Poly.html
2004/01/13
Ben Saucer has succesfully implemented this filter pair to be used in his audio effect. Here are some useful (edited) excerpts from our e-mail correspondence.
Here’s a quick diagram of the allpass pair:
................ filter 1 ................. +--> allpass --> allpass --> allpass --> allpass --> delay --> out1 | in | ................ filter 2 ................. +--> allpass --> allpass --> allpass --> allpass ------------> out2 (+90 deg)
We can use cookbook formulas to convert an allpass section into code. A general IIR recurrence relation:
out(t) = a0*in(t) + a1*in(t-1) + a2*in(t-2) + ...
+ b1*out(t-1) + b2*out(t-2) + ...
results in the transfer function:
a0 + a1*z^-1 + a2*z^-2 + ...
H(z) = ----------------------------
1 - b1*z^-1 - b2*z^-2 - ...
The allpass section in question has the following transfer function:
a^2 - z^-2
H(z) = ------------
1 - a^2 z^-2
We want to convert this into the recurrence relation. According to the cookbook formulas and the above transfer function:
a0 = a^2, a2 = -1, b2 = a^2, rest of coefficients zero => out(t) = a^2*in(t) - in(t-2) + a^2*out(t-2)
which simplifies to the one-multiplication allpass section:
out(t) = a^2*(in(t) + out(t-2)) - in(t-2)
High quality stuff! I’ve used this filter for extracting audio envelopes as abs(out1)+abs(out2) and a peak-hold filter.
It would be interesting to learn more about the theory behind it, and how the coefficients were calculated. Krukowskis site appears to have been taken offline permanently =(
Comment by David Revelj — 2010-05-05 @ 13:30
David, I don’t know well the theory behind this. Waybackmachine has some PDF’s at Artur Krukowski’s web page. The first of them cites harris, f., M. d’Oreye de Lantremange and A. G. Constantinides, “Digital signal processing with efficient polyphase recursive all-pass filters”, presented at International Conference on Signal Processing, Florence, Italy, September 4-6, 1991.
I too have used this for envelope extraction, as sqrt(out1^2+out2^2) followed by a smoothing filter. This formulation gives a flat envelope for any audio frequency sinusoid. I recall that there were some problems from the large group delay at low frequencies. Unfortunately I did not put here a phase plot to highlight that.
For calculation of the coefficients I used Differential Evolution optimization with a minmax cost function. It can be guided a bit by the fact that the a’s of the two filters are always interleaved. It is enough to look at one half of the spectrum, the other half will behave exactly the same. This symmetry is also reflected in the low amount of computations that the filters require, so it should not be broken even when requirements for the other half of the frequency response are more relaxed. It is better to keep the symmetrical structure.
Comment by Olli Niemitalo — 2010-05-05 @ 14:42